今日は音楽理論の続きで倍音について解説しましょう。
以前にも解説したことがあるのですが、今回は波形に関連させながら書いてみたいと思います。
まず、倍音とはなにか。
ギターでもピアノでもポーンと一つの音を鳴らすと特定の周波数に聞こえるのですが、その周波数の音程だけが鳴っているわけではありません。
様々な倍音が一緒に鳴っています。
倍音についてはこちらの記事をご覧ください。
簡単にまとめると、均一な素材が振動しているわけではないので、基音の2,3,4,5…倍の音がたくさん鳴っていたり、他の周波数の音もたくさん鳴っているということですね。
その倍音の含まれ方で波形が変わり、音色が変わります。
では波形の合成について書いていきたいと思います。
例えば、前回紹介した矩形波(くけいは)という波形があります。
これはシンセサイザーという楽器を使って発生させた音なのですが、基音の他に第3倍音、第5倍音、第7倍音・・・が含まれている波形です。
奇数倍音だけが含まれているということですね。
この波形を作るために波形を合成してみようと思います。
厳密に矩形波を作ろうと思ったらめっちゃややこしい計算式が出てきたので、今日は簡単な割合にして書いてみようと思います。
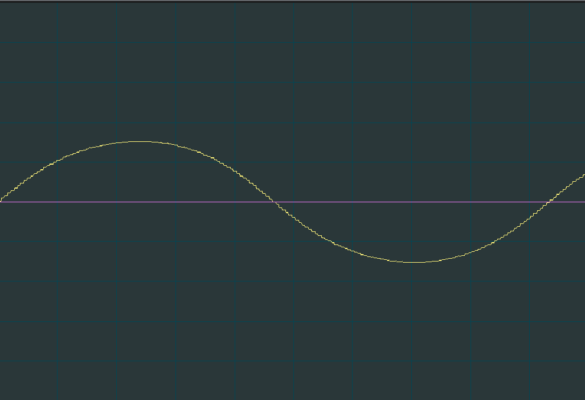
まず、基音を用意します。
一つの周波数が鳴っている状態はこのようになめらかな波形(サイン波)になります。
そこに第3倍音、波の数が3倍になったものを、波の高さを1/4ぐらいにして合成してみたいと思います。
これを合成するとこのような波形になります。
波が逆らっているところは互いに打ち消し合っているのがわかるでしょうか?
そして形もちょっと矩形波っぽくなっていませんか?
今度は基音に2倍音、波の数が2倍になったものを足してみようと思います。
先ほどと同じように1/4ぐらいの高さの波を合成するとこうなります。
ノコギリ波っぽくなっていますよね。
こんな感じですべての倍音(第1倍音、第2倍音、第3倍音・・・)を足していくとノコギリ波になります。
これが倍音と波形の関係になります。
なんとなくイメージはつきますでしょうか?
倍音を足していくと尖った波形になり、音色も尖ってくるということですね。
実際の楽器はもっと複雑な波形になりますが。







0 件のコメント:
コメントを投稿