音楽理論解説 「実際の純正律、平均律」

今日は純正律、平均律を実際の周波数に置き換えてみたいと思います。

今までは「ド」の音が100Hzだとした表を使ってきました。

しかし、実際の周波数は全然違います。

実際には「Ａ（ラ）」の音が440hzになります。

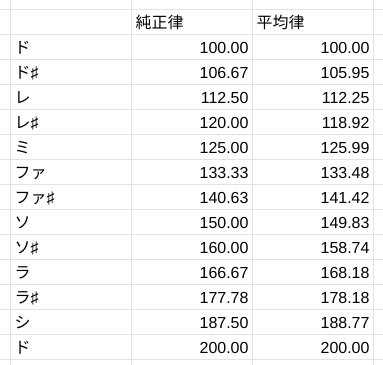
Ａを440HzだとしたＣキーの純正律と、Ａを440Hzだとした平均律を表にするとこうなります。

それぞれ計算式を一緒に書くとこうなります。

純正律の方はAを440Hzとしたので、ドとラの音が6度の関係、ド：ラ＝３：５になるようにします。
後はドから純正律の比率に則って計算していくとＣキーでの純正律の完成です。

平均律の場合はキーについて考える必要がないので、ラを440Hz、1オクターブ上を880Hzにしてその間を等比数列で並べるとこうなります。
詳しい仕組みはわかりませんが、表の右端の式が等比数列になる式のようです。
周波数がオクターブを超えた場合は半分にしています。

ちなみに、Ｄメジャースケールの純正律にするとこうなります。

純正律の方は少し周波数が変わっていますね。

平均律の方は順番が変わっただけで周波数自体は変わっていません。

なので、純正律では転調ができず、平均律は転調し放題ということですね。